CONFÉRENCE de SAVERNE
Claude Bruter, April 2010


INTRODUCTION I. CONSIDÉRATIONS GÉNÉRALES SUR LES RAPPORTS ENTRE MATHÉMATIQUES ET ARTS ou quelques dénominateurs communs aux arts et aux mathématiques II. VUE PANORAMIQUE SUR LA PRÉSENCE DES MATHÉMATIQUES DANS LES OEUVRES ARTISTIQUES À TRAVERS DEUX UNIVERSELS DE L’ART DÉCORATIF
*Illustration de couverture : Ceratites nodosus du Triassic de Saverne, France. Musée d’Histoire Naturelle, Université d’ Oslo.
|
A la mémoire de mes parents
Le texte qui suit développe la trame d’un exposé fait un vendredi après-midi devant une centaine d’élèves des premières et terminales scientifiques du Lycée de Saverne, en Alsace, le soir devant enseignants et parents. On doit à une de leur professeur de physique, Madame Marie-Cécile Dal Capello, la belle initiative locale de « bars des sciences », dont l’organisation ultime est confiée aux soins des élèves. Je ne saurais trop remercier de leur accueil, chargé de présents, Elise Muller et ses camarades, Céline, Julie, Pauline et Valentine. Bien sûr, ces remerciements s’adressent aussi à toute l’équipe administrative et pédagogique du Lycée de Saverne, qui a participé avec bonheur et compétence à la mise en place de cette journée.
Une petite citation d’Aristote, empruntée à son traité de Métaphysique, servira d’exergue à cet exposé : Les formes les plus hautes du beau, dit-il, sont l’ordre, la symétrie, le défini, et c’est là surtout ce que font apparaître les mathématiques.
L’incarnation des mathématiques dans l’art n’a cessé d’être présente depuis l’aube de l’humanité. Dans l’antiquité, on citera la construction des pyramides et des temples, la réalisation des frises et de multiples pavages, des mosaïques. Chacun a entendu parler du nombre d’or qui a fasciné tant d’artistes, le sculpteur grec Phidias sans doute, Michel-Ange et Léonard de Vinci certainement, récemment l’architecte Le Corbusier, pour ne citer que des noms célèbres. Les quinzième et seizième siècles ont connu un âge d’or, avec l’introduction par les artistes de la théorie mathématique de la descriptive, son usage en peinture, la redécouverte des polyèdres et leur inscription dans les œuvres de cette époque. Qui ne connaît pas les noms de Piero della Francesca ou de Dürer. Un nouvel âge d’or se développe au vingtième siècle et s’étoffe avec vigueur aujourd’hui. Cubistes, constructivistes font encore appel à des formes mathématiques simples, mais déjà les sculpteurs Pevsner et Gabo créent des surfaces réglées plus élaborées, Dali fait venir chez lui des mathématiciens, et Escher plonge ses œuvres parmi les plus célèbres dans la géométrie hyperbolique. En matière d’architecture, les mathématiques ont donné leurs formes au Palais du CNIT à La Défense, aux réalisations admirables des opéras de Sydney en Australie et de Valencia en Espagne. On assiste aujourd’hui à une création foisonnante d’œuvres inspirées par les mathématiques, dont l’univers est peuplé d’une infinité d’objets plus surprenants les uns que les autres. Ils sont si nombreux, si divers dans leurs propriétés que les mathématiciens sont loin de les connaître tous. Tout comme le grand public, ils ont plaisir à les découvrir dans leur éclat grâce au travail des artistes qui, par la justesse et la pureté de leurs dessins, leurs jeux des couleurs, nous font découvrir leurs beautés cachées.
Ces quelques mots d’introduction laissent entrevoir l’immensité du sujet à traiter, les rapports entre les mathématiques et l’art. Plutôt que de trop rester dans les généralités de la fresque, je me propose d’examiner plus en détail deux points : dans le premier, j’évoquerai, brièvement, quelques dénominateurs communs aux arts et aux mathématiques, dans le second, je montrerai la profondeur et l’étendue des potentialités artistiques et mathématiques contenues dans deux gravures, exécutées il y 18000 ans.
MATHÉMATIQUES ET ARTS
ou quelques dénominateurs communs aux arts et aux mathématiques
Comme entrée en matière, en préliminaire, quelques mots sur les raisons pour lesquelles les activités mathématiques et artistiques sont si profondément liées. Je retiendrai cinq points communs : 1) l’activité de représentation de l’espace, 2) le rôle de la lumière, 3) le souci de perfection, 4) l’inventivité et la fécondité, 5) l’originalité, évidemment liée à l’inventivité.
Notre point de départ sera la transposition, dans un langage plus moderne et dans une perspective plus générale, de cette simple remarque de Platon :
«la nature mortelle cherche, dans la mesure où elle le peut, à se donner perpétuité, immortalité »
C’est en effet un fait très général que tout objet, j’insiste sur le terme tout objet, s’efforce d’être placé dans les conditions qui lui assurent la meilleure permanence à travers l’espace et à travers le temps, la plus grande stabilité spatiotemporelle.
Pour assurer la stabilité de leur personne, les êtres vivants ont besoin de connaître leur environnement, pour y puiser les formes d’énergie nécessaires à leur maintien, et pour se préserver de tous les dangers qu’ils peuvent rencontrer. Ils ont développé pour cela des mécanismes et des outils de détection, et de représentation de cet environnement, de l’espace dans lequel nous sommes plongés.
1) Représentation de l’espace et ce qu’il contient
Tant l’artiste que le mathématicien participent à ce travail de représentation de l’espace et des objets qu’il contient, des phénomènes qui s‘y produisent. Ces objets, ces phénomènes concernent en premier lieu le monde physique, sur lequel s’est construit ensuite le monde biologique, sur lesquels se sont construits à leur tour les mondes psychologique, intellectuel, symbolique.
Tous ces mondes sont figurés, avec plus ou moins de présence, d’intensité, de subtilité, de profondeur, dans les œuvres si nombreuses et si diverses des artistes, qu’ils soient peintres, sculpteurs, architectes ou musiciens.
Quid des mathématiciens ? La mathématique est une sorte de miroir plein de propriétés dans lequel se reflète pour le moins la réalité physique du monde. C’est une construction à étages. Elle provient, dans ses fondements, de la représentation dans un langage quelque peu symbolique d’objets et de phénomènes du monde physique, souvent liés entre eux par des relations de causalité. Ces représentations sont étudiées par elles-mêmes, le déroulement des causalités permettant la monstration de faits parfois peu apparents. Des expériences de pensée conduisent à poser de nouveaux problèmes, à fabriquer de nouvelles représentations, à découvrir le caractère général de certaines méthodes, de certaines propriétés. Au second étage, on étudie le mode de génération et la structure de ces représentations premières ; c’est la part qui paraît la plus abstraite des mathématiques. Par voie de retour, ces études permettent d’enrichir la connaissance de faits, d’apporter la preuve causale de leur existence.
Je laisserai à un artiste le soin de clore cette petite section consacrée à l’espace, ses propos révèlent à quel point il avait conscience de la nature de son activité :
« mon lecteur attentif sait, aussi bien que moi, que tout ce qu’il y a de réellement superfin et sensationnel à notre époque provient spécialement de l’évolution de l’idée de l’espace, laquelle, comme tout le monde peut se le rappeler, ayant commencé par n’être qu’une espèce de nourriture abstraite, sans goût ni substance, a fini – comme nous allons le voir immédiatement – par devenir, de nos jours, un des plats les plus succulents et épais de la pensée contemporaine.
L’espace, pour Euclide, d’après qui l’intersection, le point, le plan n’étaient pas autre chose que des objets matérialisés, l’espace, dis-je, n’arrivait pas pour lui à atteindre une consistance supérieure à celle d’un léger bouillon de tapioca parfaitement utopique et refroidi.
C’est avec Descartes que, par la considération de l’espace comme un contenu à trois dimensions, commence à épaissir le jus insipide et encore, et surtout, à ouvrir l’appétit aux expectation salivaires qui provoquent déjà cette extravagante cuisine de l’espace ; laquelle trouve définitivement tout son poids avec la pomme de Newton qui, comme on le sait, était un savant ayant, déjà, indiscutablement, une inertie et une famine considérables. » (Salvador Dali)
2) Rôle de la lumière
La lumière est la première des sources d’énergie, et c’est principalement par sa présence que s’accomplit la détection des objets, la reconnaissance des formes, leur première caractérisation. Le rôle de la lumière est un autre de ces dénominateurs communs entre mathématiques et arts.
La géométrie classique est avant tout l’étude des ombres sur des écrans des objets éclairés par des faisceaux lumineux. Le théorème attribué à Thalès (636-546) est l’énoncé fondateur de la géométrie. C’est en fait une observation de base de l’optique géométrique, du monde physique le plus accessible à nous.
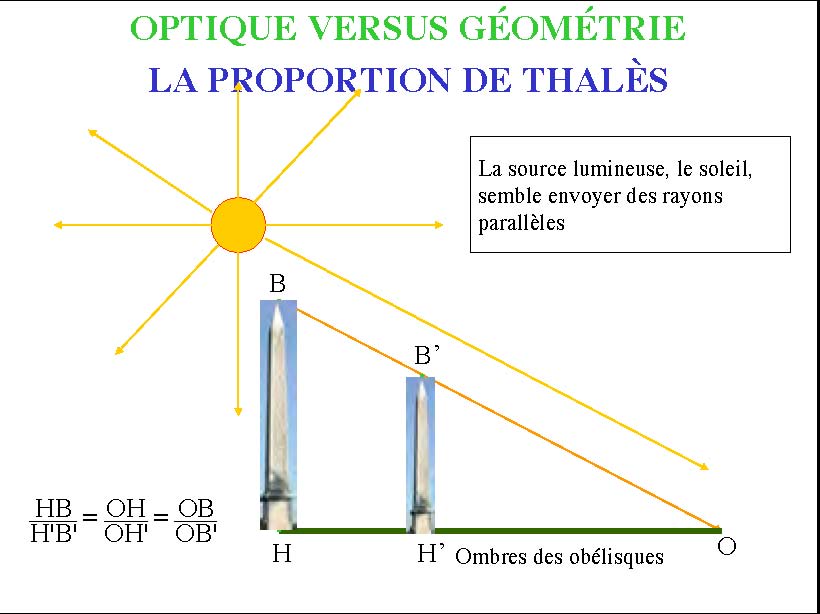
La toile du peintre est également cet écran sur lequel se projettent, portés par les rayons de lumière, ses visions du monde, comme nous le rappellent par exemple ces deux gravures classiques (1525) d’Albrecht Dürer (1471-1528).


Empruntons ici au poète ces quelques vers évoquant l’arrière-plan lumineux fondateur et commun aux activités géométriques et artistiques :
Ne dis plus rien Ne pense à rien Les lumières bleutées des réverbères Qui sculptaient nos ombres sur la terre …
Notons que dans ce domaine de la lumière, le peintre va plus loin que le mathématicien, en ce sens qu’il ajoute la couleur à la forme pour rendre l’objet plus présent, parfois plus significatif. Mais, dans ce même domaine, le mathématicien va également plus loin que l’artiste, car son étude de la forme est plus précise, plus complète, et finalement le conduit à enrichir de manière considérable la panoplie des formes.
3) Le souci de la perfection
Par ailleurs, mathématicien et artiste n’ont-ils pas en commun le souci de finition dans l’exécution ? L’exactitude, la précision, la perfection dans la réalisation sont souvent l’apanage de l’artisan digne de ce nom, de l’artiste.

Immortality (nœud de trèfle) John Robinson (sculpteur 1935-2007)

(2x² + y² + z² - 1)3 – 1/10 x²z3 – y²z3 = 0 (Tore Norstrand & Bruce Hunt)
Comment alors celui-ci ne serait-il pas séduit par la pureté de la ligne tracée par le mathématicien, la rigueur de sa description et du dessin qui en résulte ? Doit-on s’étonner de l’attraction exercée par le monde des objets mathématiques sur nombre de graveurs depuis Dürer jusqu’à Jeener en passant par Flocon ? Et n’oublions pas les magnifiques gravures sur pierre exécutées par les Egyptiens pendant plusieurs millénaires.

Pavage d’hypercube, Patrice Jeener
https://www.mathart.eu/jeener/index.html
4) L’inventivité, la fécondité
Quel que soit le domaine d’activité considéré, le grand homme est celui qui laisse derrière lui une œuvre abondante. C’est le cas des grands artistes, des grands mathématiciens. Sait-on par exemple que l’on n’a pas fini de publier les écrits du grand Euler (1707-1783), cet empereur des mathématiques : ses œuvres en 76 volumes auront fini de paraître cette année, il restera encore à publier sa correspondance qui devrait occuper 9 volumes supplémentaires.
Souvent l’artiste, par la puissance de son imagination, nous met au contact de spectacles inattendus, insolites parfois, exaltant et déployant les possibilités du monde actuel.
C’est souvent le cas des tableaux de Salvador Dali (1904-1989). Mais se cachent toujours, plus ou moins, dans ses tableaux, la présence de faits mathématiques. Dans celui-ci, on observera la simple présence de deux axes de symétrie, assurant, selon la dénomination des mathématiciens, des réflexions miroirs : le premier axe, vertical, passe par le point de fuite du tableau, situé près de cette petite barque centrale, et d’où rayonne la lumière qui inonde le paysage. Le second axe de symétrie, horizontal, passe par le milieu du lac, en lequel se reflètent trois cygnes ; derrière eux des troncs d’arbres se contorsionnent dans le ciel : le reflet dans l’eau de cet ensemble fait voir trois éléphants sur lesquels les cygnes semblent assis.
On est bien ici en présence d’inventivité, et d’inattendus insolites.

S. Dali, Cygnes réfléchis en éléphants, 1937
Mais les mathématiques n’en font-elles pas autant, sinon davantage, grâce aussi à l’infinie potentialité du nombre. La métaphore suivante le fait voir aussitôt. Chacun connaît aujourd’hui l’énoncé du théorème de Pythagore:
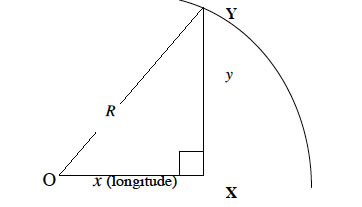
si x désigne la longueur du côté OX du triangle OXY, rectangle en son sommet X, y la longueur du côté XY, et R la longueur de l’hypoténuse OY, alors le carré de la longueur de cette hypoténuse est égale à la somme des carrés des longueurs des deux autres côtés :
R²= x²+ y²
Lorsque x et y varient de sorte la relation x²+ y²= R² reste toujours vérifiée, le point Y décrit un cercle de centre O de rayon R.
Maintenant, remplaçons le 2 qui montre le carré de x par un nombre quelconque n, le 2 qui montre le carré de y par un nombre quelconque m, le coefficient 1 qui affecte x² par un entier positif ou négatif quelconque p, le coefficient 1 qui affecte y² par un entier positif ou négatif quelconque q, de sorte qu’on obtient l’expression
px n+ qy m= R²
Cette expression toute simple définit une infinité de formes possibles puisque chacun des nombres p, q, n et m peut varier à l’infini.
Shakespeare me pardonnera peut-être d’adapter à notre modernité sa célèbre remarque : « Il y a plus de choses sur la terre et dans les mathématiques, Horatio, qu’il n’en est rêvé dans votre philosophie ».

T8(x) + T8(y) + T8(z) = 0 avec T8(x) =128x − 256x + 160x − 32x² + 1.
Une surface de Chmutov de degré 10 avec 345 points singuliers (Bruce Hunt)

https://www.imaginary2008.de/galerie_view.php?gal=1
Sextique de Barth déployée à 65 Singularités 4(Φ²x²-y²)(Φ²y²-z²)(Φ²z²-x²)-(1+2Φ)(x²+y²+z²-w²)² w² == 0 Φ est le nombre d’or, w un paramètre au-dessus égal à 1, en dessous égal à 0

https://virtualmathmuseum.org/Surface/barth_sextic/barth_sextic.html
Ainsi, à l’extrême diversité des œuvres artistiques, répond la richesse morphologique infinie de l’univers mathématique.
5) L’originalité
Un autre point commun entre objets mathématiques et œuvres artistiques est leur caractère surprenant, inattendu, qui éveille la curiosité, attire le regard, et parfois fascine : l’œil, la pensée sont séduits par l’originalité singulière et sans cesse renouvelée.
L’œuvre d’art est souvent cette alliance réussie entre la singularité de la forme, la pureté de ses lignes et l’infini nuancier de la lumière incarnée dans la matière. Cette alliance peut séduire tant l’artiste que le mathématicien. Si l’un comme l’autre peuvent s’attacher à ne révéler, dans sa pureté fascinante, qu’une seule forme mathématique, la fécondité de leur imagination peut également les conduire à créer des œuvres originales peuplées d’objets variés révélant la chaleureuse richesse de l’univers des formes.

Projet d’affiche pour la Première Conférence de l’ESMA, J.Constant, 2010
Pour conclure cette première partie, je ferai appel à cette œuvre d’Henri Rousseau, dit Douanier Rousseau (1844-1910) :

Le lion ayant faim (Douanier Rousseau, 1905)
Cette toile, nous rappelant quelque peu la forêt vierge et l’abondance qui la caractérise, ne symbolise-t-elle pas la fécondité de la nature et l’originalité de ses créations ?
DANS LES ŒUVRES ARTISTIQUES À TRAVERS
INTRODUCTION GÉNÉRALE
Il ne semble pas que les spécialistes de l’histoire de l’art, les critiques, aient jamais attiré l’attention de leurs lecteurs sur la présence d’universaux dans la décoration. Pourtant, deux d’entre paraissent s’imposer à l’évidence : il s’agit de la présence du motif spirale comme premier universel ; le second universel est celui de la création et de la réalisation constante de pavages.
L’explication de la présence de ces deux universels repose essentiellement sur la sensibilité de l’être humain aux grands phénomènes de la nature, à son activité de représentation de ces phénomènes, évoquée dans la première partie.
Le premier d’entre eux est celui du mouvement. L’un des mouvements parmi les plus importants se trouve être celui en forme de spirale : il donne naissance à une représentation récurrente dans l’art décoratif.
Une seconde question d’importance est celle du contenu de l’espace, de la manière dont il est constitué, et se constitue. La création de pavages est une façon plus ou moins consciente d’illustrer cette question, de suggérer une voie de réponse.
Les chapitres qui suivent vont quelque peu reprendre, développer et étayer ces points de vue.
I.1 Préliminaire : présence du mouvement spiral
On a toujours fait, au moins depuis Aristote (384-322), la distinction entre l’inanimé et l’animé. Nous avons, dans l’immédiat, une meilleure connaissance de l’inanimé, de l’objet fixe, qui se laisse observer plus longtemps. Nos connaissances sur l’inanimé ont été beaucoup longues à s’établir ; ce sont elles pourtant qui nous auront permis d’accomplir les plus grands progrès sur le plan technologique et sur le plan de la compréhension, car le figé n’est qu’une singularité stabilisée au sein de l’évolution. C’est donc du mouvement que je vais parler d’abord.
Selon Aristote encore, il existe dans l’univers deux mouvements fondamentaux, le rectiligne et le circulaire. Ils engendrent, selon l’expression du Stagirite, des mouvements mixtes. On doit au mathématicien Joseph Liouville, qui vivait au XIXéme siècle, la démonstration de cet énoncé dans le cadre général des espaces multidimensionnels : tout mouvement local est la composition d’un mouvement rectiligne et d’un mouvement circulaire. Mais c’est dans l’œuvre d’Aristote que je viens de citer, dans le tome VIII du traité qu’il consacre à la Physique, que ces faits sont mentionnés pour la première fois dans des écrits. Aristote ajoute que le circulaire est nécessairement antérieur au rectiligne. Les raisons qu’il avance peuvent nous paraître naïves ou spécieuses, elles répondent en tout cas à une intuition physique profonde.
Accorder la primauté au mouvement circulaire implique sa plus grande présence dans la composition du mixte. C’est ce que confirme l’observation du monde physique : on n’y observe jamais que des portions de trajectoires rectilignes.
En dehors du circulaire et du rectiligne fondateurs, existerait-il, dans notre univers physique, des formes de trajectoires qui apparaîtraient plus fréquemment que d’autres, qui seraient sans doute plus significatives car plus proches de la réalité physique ?
Il en est une qui vient rapidement à l’esprit, et cela parce qu’elle présente des caractères d’universalité et de stabilité tout à fait remarquables, qui en font l’un des archétypes des formes du mouvement : c’est la trajectoire associée à un mouvement de création et de façonnage qui vient s’immobiliser au moment où le stade final est atteint.
Ce type de trajectoire est présent dans tous les règnes de la nature. Nous le rencontrons d’abord au sein de l’univers physique primordial, par exemple dans cette image obtenue récemment de la galaxie du Tourbillon :


Cette forme de trajectoire, on la retrouve dans le dessin des coquillages, des cornes de divers quadrupèdes, des appendices allongés de certains singes, des vrilles des vignes, des enroulements de feuilles, de l’ADN, de la cochlée etc. Elle nous est familière, naturellement conduite par le mouvement de rotation spontané du poignet.
Aussi, l’artiste qui est instinctivement conduit à représenter les phénomènes de la nature parmi les plus insistants, a-t-il fait figurer cette forme primordiale dans ses décors, depuis les temps les plus reculés.
La forme spiralée est donc bien un universel de l’art décoratif.
I.2 Les spirales dans le monde l’art
La Bradshaw Foundation s’emploie à mettre à jour les œuvres d’art du passé lointain de nos sociétés. Les gravures rupestres témoignaient certes des capacités des hommes à produire des figures stylisées, d’animaux familiers pour l’essentiel. Mais les deux gravures sur ivoire suivantes, parmi les plus remarquables de notre point de vue, témoignent de la rationalité dont les hommes faisaient preuve. Voici des images de ces deux objets, façonnés il y a près de 18 000 ans, et découverts en Sibérie, près du lac Baikal :
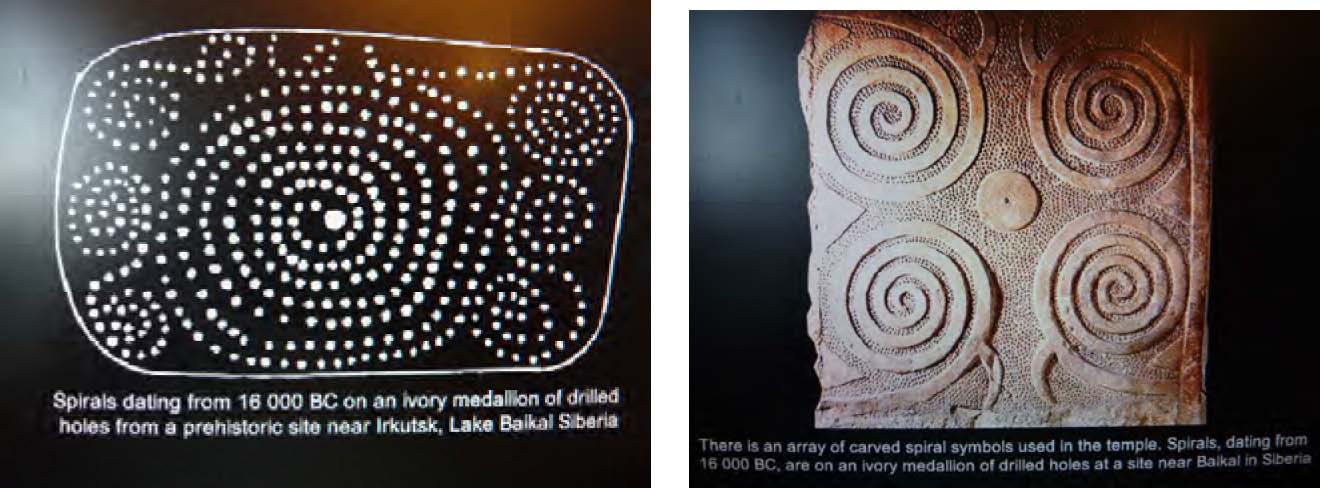
Ces œuvres sont emblématiques : présence de la symbolisation de trajectoires fondamentales sous la forme de spirales et de doubles spirales, symétrie, motif répété, pavant l’espace. Elles portent en elles de manière potentielle, elles symbolisent, sur le plan artistique, toute l’histoire et le contenu du décor, sur le plan physico-mathématique, toute l’histoire et le contenu des recherches sur la description des mouvements, et sur les manières dont la Nature remplit l’espace.
On peut sans doute voir dans la partie centrale du premier objet, en arrièreplan, la représentation d’une assemblée réunie autour d’un chef, mais le caractère spiralé de la représentation, la symétrie qui l’accompagne sont l’expression d’une rationalité plus orientée vers l’abstraction, mais où néanmoins se déploie une imagination créatrice.
Le second médaillon se singularise également par sa plus grande perfection artisanale, une plus grande recherche dans le jeu des symétries, ici croisées. Mais on voit également ici, et surtout, un domaine occupé par des formes identiques, à quelque chose près. De manière implicite, l’artiste, l’homme aborde une problématique essentielle, déjà traitée par Platon : comment la nature remplitelle l’espace ? Une vision peut-être encore naïve et illusoire donne à penser que l’espace serait entièrement rempli de particules identiques, en quantité incommensurable. La fabrication de pavages des sols est une expression simplifiée de cette problématique et de sa solution. C’est dans un second temps que cette question sera abordée.
Mais d’abord, voyons rapidement, par l’image, la manifestation persistante, à travers les siècles, de la présence de la trajectoire fondamentale, la spirale, dans quelques-uns des décors conçus par les artistes.
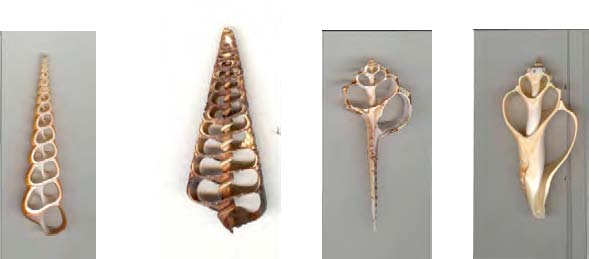
Coupes de Coquillages offerts par Nat Friedman



Motifs égyptiens (extraits de l’ouvrage d’Ipppolito Rosellini, « Monuments de l’Egypte et de la Nubie » (dessins de l’expédition franco-tocane de 1828), Bibliothèque des Introuvables, Paris, 2007)

Cratère de Vix, - 510 à comparer au vase macédonien qui suit

Epoque d’Alexandre, vers - 320

Période grecque (Musée de Tel Aviv)

Historiska Museet, Stockholm Le Livre de Durrow (Irlande 7ième siècle)

Période Ming

Œuvre Arménie Athanasius Kircher, 1679 (1602-1680)

Pieter Brueghel artiste flamand (XVIéme) (v. 1525-1569)

Musée du Louvre
VINGTIÈME SIECLE

La nuit étoilée à St-Rémy 1888 Van Gogh (1850-1890) 1923

10, Bd de Port-Royal, 6ème (G. Jacquet 1937) 3, rue Mouthon, 15ème

Dali La Madone de Rafael à la vitesse maximum, 1954
Le commentaire explicatif sur cette œuvre sera donné par son auteur lui-même dans le paragraphe qui conclut ce chapitre consacré aux spirales.

1957 1958 1953 Mauritz Escher

Richard Long (2008) Dominique Ribault
Jean Constant (1998-2003)
https://www.hermay.org/jconstant/dspires/spires.htm

Jean-François Colonna, Coquillage quaternionique (2006)

Ulrich Eitner 2006 (Surface de Bonnet)
https://www-sfb288.math.tu-berlin.de/Research/PAINLEVE/Bonnet.html
Hormis les deux dernières images, celles-ci sont extraites du site :
https://home.nordnet.fr/~ajuhel/Surfaces/quad_archi_hel.html

Aphrodisias (Turquie) Rome, la colonne Trajane

Minaret hélicoïdal (52 mètres de haut) de la mosquée d'al-Mutawakkil (848-852) & Église Saint-Séverin, Paris (XVème siècle)


Turfan (Chine): mosquée d'Emin. Istanbul (Turquie), Sainte-Sophie


Colonne Vendôme, Paris

Tour nommée Turning Torso à Malmö (Suède) (Calatrava 1999-2004)
I.3 Deux importantes spirales mathématiques
Un mot bref sur la représentation mathématique des spirales parmi les plus anciennes et les plus intéressantes, que sont les spirales archimédiennes d’une part, les spirales logarithmiques d’autre part.

On doit à Archimède (-287, -212), ou à son disciple Conon de Samos, la première description mathématique d’une spirale plane fort régulière. Si on choisit un point origine O dans le plan, on note en général par ρ la distance de O à un point courant M de la spirale. OM fait un angle θ avec une droite fixe passant par O.
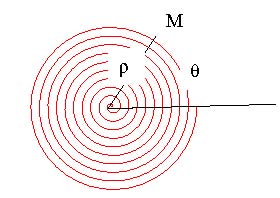
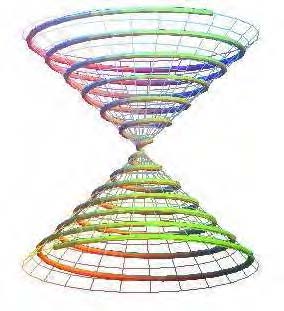
Pour la spirale d’Archimède, la distance ρ est proportionnelle à l’angle : ρ= a θ
Relevée sur un cône droit de base circulaire, elle porte alors le nom de spirale de Pappus (4ième siècle).
On appelle maintenant spirale archimédienne toute spirale dont l’équation est de la forme
ρn = a θm+ b
On ne connaît pas d’étude sur les spirales autre que celle d’Archimède avant le 17ème siècle. En ce siècle, se développe pour la première fois l’étude rationnelle et mathématique du mouvement et de la mécanique. Fermat (1601-1665) en 1736 est le premier successeur d’Archimède. Il étudie d’une part le mouvement d’un mobile à l’intérieur de la terre soumis à une accélération constante, et d’autre part celui d’un mobile dont l’aire balayée par le rayon vecteur OM est proportionnelle au carré de l’angle de rotation. Il donne ainsi les équations de deux nouvelles spirales archimédiennes.
En 1638, Descartes (1596-1650) introduit la spirale logarithmique : le rayon vecteur OM coupe la trajectoire de M sous un angle V constant.
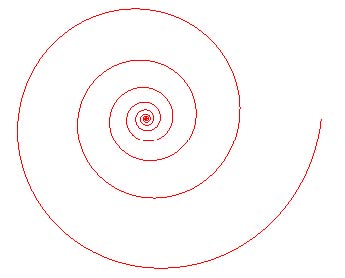
Newton (1642-1727) la fait apparaître dans ses Principia (1686) :
« en présence d’une résistance de l’air de masse volumique inversement proportionnelle à la distance OM = r, un mouvement possible dans un champ central en 1/ rn, était une spirale logarithmique (propositions XV, XVI, et XVII) ».
Son équation s’écrit de manière générale : θ/tgV
ρ= a eou encore Log ρ= b θ.
En donnant à a la valeur du nombre d’or Φ, à tgV la valeur de π, on rencontre cette spirale quelquefois incarnée approximativement dans la nature :

Cyclone polaire au large de l’Islande Whirlpool Galaxy (M51A/B or NGC 5194/5) NASA/ESA

Détail d’une fleur de tournesol Coupe sagittale d’une coquille de nautile http ://fr.wikipedia.org/wiki/Spirale_logarithmique
Par ailleurs
« La spirale logarithmique fut souvent utilisée par l’homme, notamment dans les constructions architecturales, tels certains clochers, jardins, paysages, allées de châteaux ou belvédères, dans lesquels la forme en ouverture confère à l’édifice une dimension d’infini. »
Cette spirale a beaucoup de propriétés inattendues, au point que Jacques Bernoulli (1654-1705), qui l’a beaucoup étudiée, l’a qualifiée de « spira mirabilis ». Il a souhaité la faire graver sur sa tombe, de même qu’Archimède avait fait sculpter sur sa tombe un cylindre et une sphère – le graveur a en fait tracé une spirale d’Archimède.

Les spirales considérées jusqu’à présent sont des courbes planes dont nous n’avons pas donné de définition générale. Nous adopterons la suivante : un élément de spirale plane est un élément de courbe d’équation ρ= f(θ) définie sur un intervalle [θi-1, θi] sur lequel f est non croissante ou non décroissante. Elle peut donc être localement stationnaire. Une spirale plane sera une courbe plane dont tout élément est lui-même spiralé. Avec cette définition, un cercle fait partie de la famille des spirales. Une telle définition s’avère nécessaire, mais non suffisante, pour traiter en toute généralité certaines courbes tracées sur des surfaces qu’on peut également considérer comme des spirales dans un sens plus large que le sens habituel.
Un élément de courbe spirale dans l’espace usuel sera alors caractérisé par le fait que sa projection sur un plan convenable est un élément de courbe spirale plane, et par le fait que l’angle de cet élément de courbe avec un plan parallèle à ce plan de référence, pour une direction de parcours adaptée, ne saurait être décroissant.
Sur les surfaces de révolution, les courbes de plus courte distance joignant deux points, ont des formes spiralées au sens général du terme.
L’exemple qui suit, d’un intérêt premier en physique, est également riche d’enseignement sur le plan mathématique. Il nous montre la projection, sur les trois plans de référence, d’une spirale dans l’espace usuel.
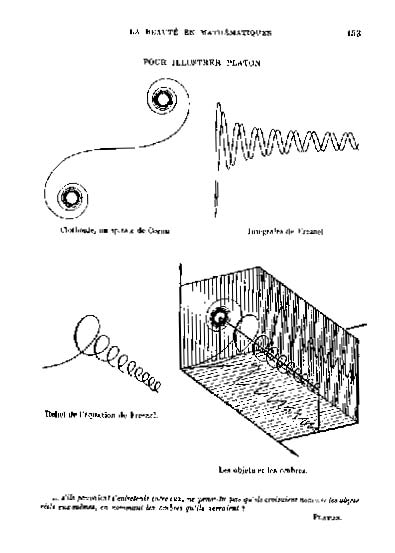
Extrait de l’article de François Le Lionnais « La Beauté en Mathématiques » in Les Grands Courants de la Pensée Mathématique, Blanchard ,Paris 1962
La figure montre également une clothoïde ou spirale de Cornu, étudiée en premier par Jacques Bernoulli. Utilisée en physique de la diffraction par Cornu (1841-1902) pour le calcul d’intégrales de Fresnel, elle sert aujourd’hui pour le dessin des voies ferrées et des autoroutes.
Un moyen simple, on peut le compliquer à souhait, pour obtenir une famille de points Mn placés sur une spirale plane consiste à fabriquer la suite
(a ρ, θ), (a ρ², 2θ), (a ρ3, 3θ),…, (a ρn, nθ), …
Les couples z = (ρ, θ) , z² = (ρ², 2θ), etc…, s’appellent des nombres de Chuquet-Cardan (on disait, autrefois, des nombres complexes) dans leur présentation d’Euler ou eulérienne.
Ces spirales jouent enfin un rôle important dans toutes les études de dynamique qualitative comme quantitative. L’équation la plus simple associée à un mouvement, l’équation linéaire x’t = Ax, définit, pour des valeurs convenables de A, la forme des plus illustres des spirales, celle des trajectoires logarithmiques, dont le point central dans cette figure, selon le mode d’évolution, peut être attractant lorsqu’on se dirige vers lui, ou au contraire répulsant lorsqu’on s’en évade.

I.4. Conclusion sur les spirales par Salvador Dali
Je ne résiste pas, pour terminer cet aperçu sur la présence des spirales dans les mathématiques et dans les arts, au plaisir de citer à nouveau le fondateur de la méthode paranoïaque-critique, le grand Salvador Dali :
« Mais soudainement je découvris que, dans les entrecroisements des spirales qui forment le tournesol, il y a évidemment le galbe parfait des cornes de rhinocéros.
Maintenant les morphologues ne sont pas du tout sûr que les spirales du tournesol soient de vraies spirales logarithmiques ; ce sont des spirales qui approchent beaucoup, mais il y a des phénomènes de croissance qui font qu’on n’a jamais pu les mesurer avec une exactitude rigoureusement scientifique ; et les morphologues ne sont absolument pas d’accord si ce sont des spirales logarithmiques ou non.
Mais, maintenant, je me suis renseigné à propos de la corne du rhinocéros elle-même : alors là, il n’y a aucun doute, il n’y a jamais eu dans la nature un exemple plus parfait de spirale logarithmique que dans le galbe de corne de rhinocéros. »
Je recommande de poursuivre la lecture du texte de Dali, lorsque, quelques pages plus loin, il analyse avec intérêt une peinture de Raphaël, puis reprend ses considérations farfelues sur son obsession rhinocentrique. En particulier, sa description mathématique d’un rhinocéros vu de dos n’est pas piquée des hannetons.
II. Comment la Nature remplit-elle l’Espace
II.1 La problématique du pavage
Je reviens maintenant sur cette problématique qui intéresse le physicien, le mathématicien, l’artiste. Soit l’espace usuel, que nous disons de dimension topologique 3, peut-on le remplir sans laisser de vides par des particules identiques, des cristaux, des photons, identique pouvant vouloir dire ayant même type de forme ? Cette question a été abordée par le cristallographe Bravais en 1847. Nous allons examiner ici le cas de la dimension plus petite 2. Un espace de dimension topologique 2 est ce que nous appelons d’ordinaire une surface, dont une réalisation matérielle est par exemple le sol sur lequel nous marchons. Donc un tel sol, un tel plan de travail de cuisine, un mur d’une salle de bains, de telles surfaces peuventelles être comblées, sans laisser de vides, sans qu’elles chevauchent, par des courbes identiques, ou bien par des domaines surfaciques identiques, comme par exemple des carrés ?
II.2 Pavages anciens (égyptiens, arabo-andalous)
Les artistes ne se sont pas intéressés à la question du remplissage d’une surface par des courbes de forme identique. Les mathématiciens, si, leur réponse ici est simple : on peut remplir les surfaces classiques à l’aide de courbes fermées sur elles-mêmes comme le sont les cercles. Dans leur langage codé, ils parlent de feuilletage de ces surfaces par des cercles, ils disent encore que ces surfaces sont fibrées en cercles. Passons.
Par contre, depuis des temps très lointains, les artistes se sont employés à fabriquer des dallages qui couvrent les surfaces, qu’elles soient des sols, des murs, tissus ou tentures. Nous avons déjà rencontré la gravure en ivoire trouvée près du lac Baikal où l’on a vu un motif en forme de spirale recouvrir une portion de domaine plan. Nous avons alors vu aussi, réalisés par des artistes égyptiens, des remplissages de domaines plans par de petits domaines identiques où figuraient des spirales.
Voici d’autres pavages de cette même origine égyptienne :

Autres types de pavages fort célèbres, ceux réalisés à l’Alhambra en Espagne, au milieu du 14ième siècle, par l’école arabe de Granada. Le minéralogiste russe I.S. Fédorov a montré en 1891 que, d’un point de vue algébrique, il ne peut exister que 17 types de groupes de pavages, ils sont représentés sur les murs de l’Alhambra à Granada.

II.3 Pavages modernes
Voici maintenant une collection de pavages du plan réalisés par le mathématicien, Mikael Field :



https://www.math.uh.edu/~mike/ag/art.html
Les deux pavages qui suivent sont dus aux mathématiciens David Austin, Bill Cassselmann et David Wright. Le premier décrit un pavage dit de Penrose (de type 2, cf https://fr.wikipedia.org/wiki/Pavage_de_Penrose) présentant de manière périodique une série de motifs pentagonaux. Le second réalise un remplissage d’un domaine circulaire par d’autres domaines circulaires, évidemment de tailles plus petites.
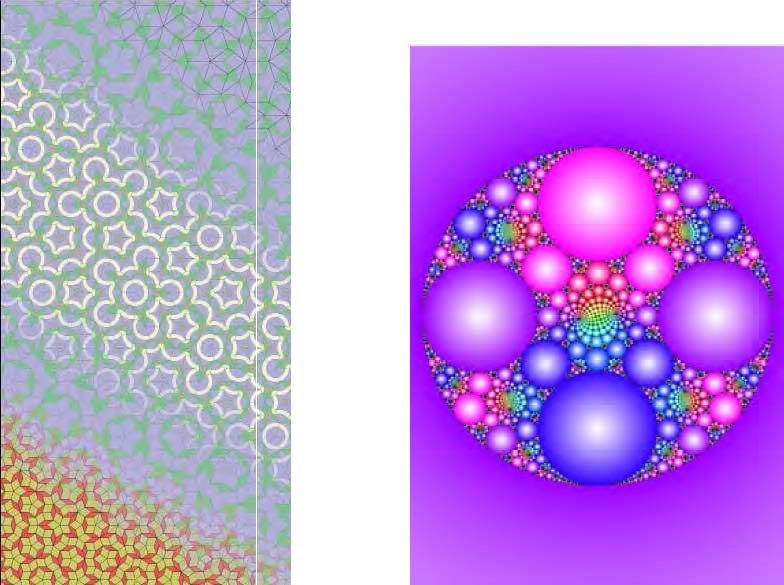
L’image de Jos Leys que nous avons déjà vue à propos des spirales est un autre pavage de ce domaine circulaire par des domaines du même type.
Il existe d’autres pavages de tels domaines circulaires mais provenant de considérations différentes. Au lieu de nous promener dans une plaine, sur une partie de la surface de la terre qui nous paraît localement plate, allons dans les montagnes, où nous franchissons un col. A notre droite et à notre gauche la montagne se relève, elle monte derrière nous vers nous, et redescend, devant nous. La forme locale de la montagne est ici celle d’une selle de cheval, que les mathématiciens appellent, par dérision sans doute, une selle de singe. La géométrie de cette partie de la montagne est dite hyperbolique. Différentes figures peuvent posséder ce type de géométrie : chacune en est une représentation. L’une d’elles est un domaine circulaire muni de propriétés ad hoc, appelé disque de (Beltrami-)Poincaré. Il peut être pavé par des polygones dont les côtés sont soit rectilignes soit des portions de cercles.
Voici deux tels pavages exécutés par Escher (1898-1972),

https://www.josleys.com/show_gallery.php?galid=325
et d’autres images artistiques sur fond de pavage hyperbolique réalisées par Jean Constant:

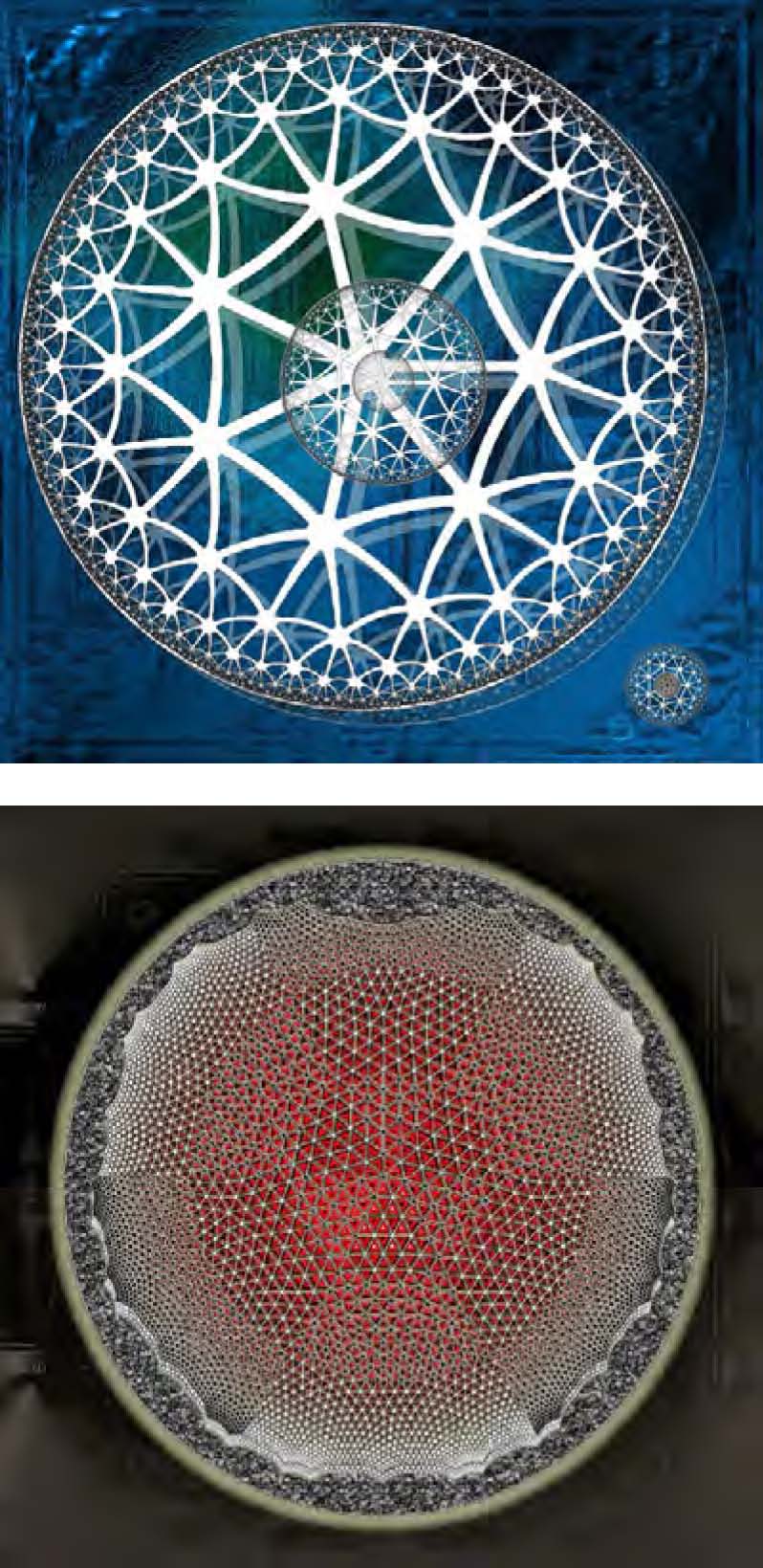
https://www.hermay.org/jconstant/animation/animhyperboles.html
Escher a également fabriqué des pavages des polyèdres platoniciens. Voici ici d’autres images fabriquées par ordinateurs faisant apparaître des pavages sur la sphère ou sur une surface nouée en nœud de trèfle :
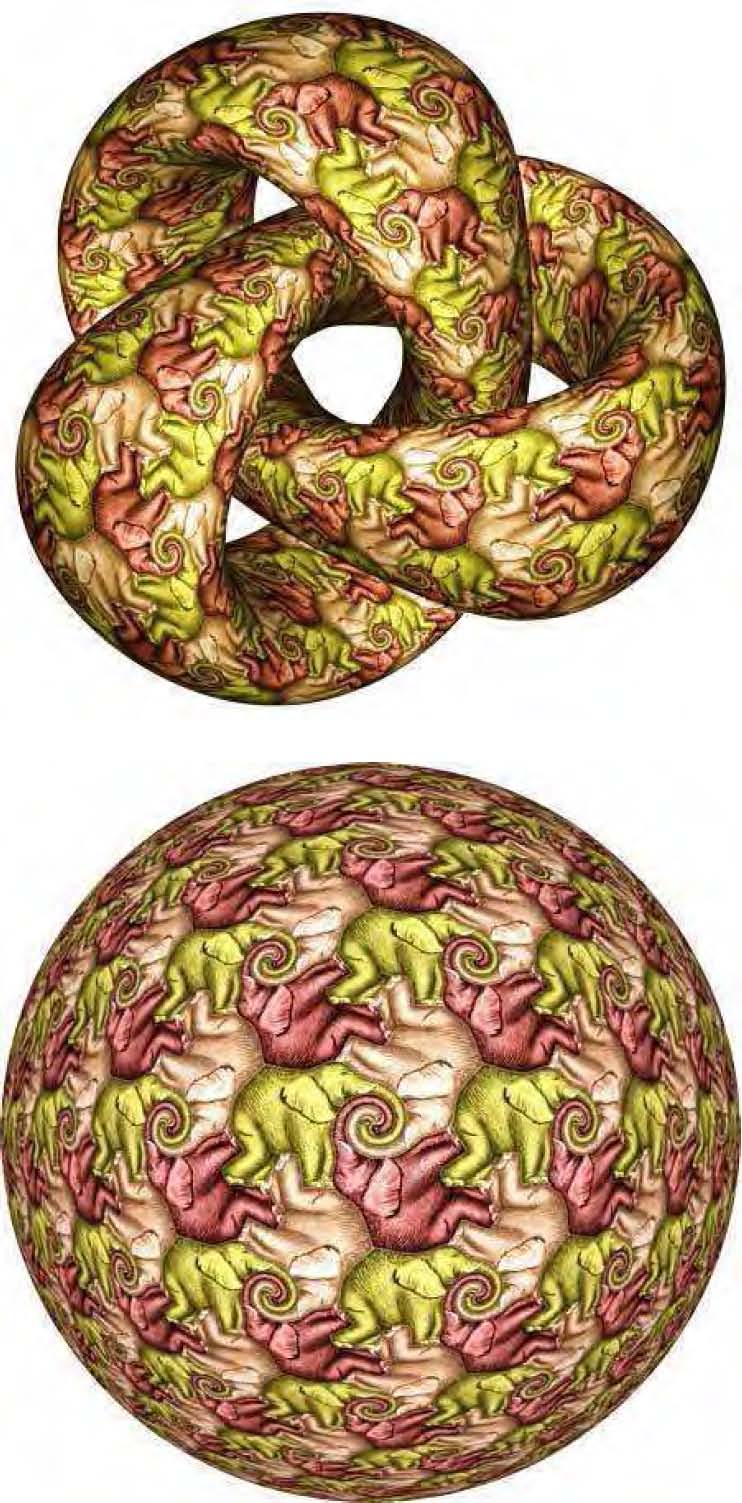
Comment réaliser un dallage sans qu’il y ait de vide entre deux dalles, y aurait-il plusieurs façons de procéder ?
Ces questions sont aujourd’hui classiques, parfaitement résolues, de très nombreux sites leur sont consacrées :
https://xahlee.org/Wallpaper_dir/c5_17WallpaperGroups.html
https://pagesperso-orange.fr/therese.eveilleau/pages/truc_mat/indexF.htm
II.4 Principes de la fabrication des pavages
Voici quelques indications sur le procédé général d’étude employé aujourd’hui.
Pour fabriquer physiquement un dallage, les carreleurs disposent d’un stock de dalles. Une dalle posée, ils prennent une autre dalle de leur stock, la déplacent près de la dalle posée, et par translation ou rotation la font jouxter cette dalle posée.
Ce sont ces mouvements qui ont d’abord été reconnus et étudiés par les mathématiciens. Ils jouent aujourd’hui un rôle essentiel dans la description de l’univers géométrique.
Reconnaissons d’abord, dans ces mouvements, les mouvements primordiaux énoncés par Aristote : un mouvement rectiligne de longueur fixée n’est autre qu’une translation, un mouvement circulaire d’angle fixé n’est autre qu’une rotation.
Remarquons que les translations et les rotations peuvent se composer entre elles, ce que fait en général le carreleur. La structure de ces ensembles de déplacements, soumis à ces compositions internes, porte le nom de structure de groupe.
Il est remarquable que ces mouvements, translation et rotation, soient le résultat d’opérations de réflexions optiques, c’est-à-dire de symétries par rapport à un miroir.
Symétrie simple : une réflexion, la symétrie ρM par rapport au miroir M :
| M | |||
|---|---|---|---|
| D | |||
| S | N | ||
ρM(N) = S, ρM(S) = N.

Conception et Réalisation par Maria DEDÓ (Milano)
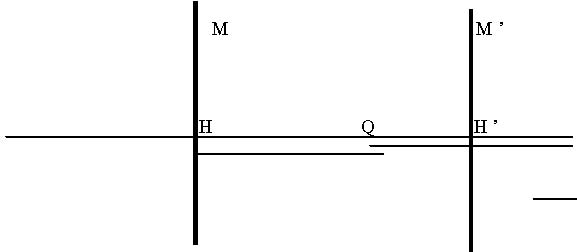
Translation : deux réflexions, la translation t de longueur 2θ en dimension 2 dans la direction d :
Soient, dans le plan usuel, P un point, M et M’ deux miroirs parallèles, perpendiculaires à la direction d, et distants de la longueur HH’ = θ.
P P’
d
Rotation : deux réflexions, la rotation r d’angle 2θ en dimension 2 de centre O :
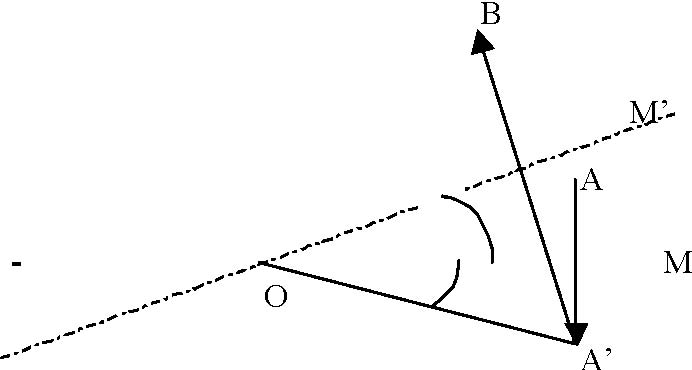
La symétrie, « hypnose divine de la géométrie de l’esprit » disait Dali, est un phénomène optique : l’objet que nous voyons par réflexion dans le miroir est le symétrique de celui que nous tenons à la main. Un symétrique se construit par réflexion. Il est remarquable qu’on puisse également décomposer et recomposer toute translation et toute rotation à l’aide de réflexions sur des miroirs convenablement placés. On retrouve ici le rôle fondamental et sous-jacent de la physique de la lumière dans la compréhension et dans la description de l’univers mathématique.
Pour fabriquer un pavage, on utilise de manière convenable toutes ces symétries, ou tous ces jeux de réflexion comme vous voudrez les appeler. Je ne vais pas détailler les 17 façons distinctes de les employer, simplement présenter une des plus simples d’entre elles, celle associée à la translation.
Le dessin suivant, que j’emprunte sans sa permission à un prix de Rome, passionné de pavages, Raoul Raba, nous montre comment on fabrique en pratique un pavage par translation. On utilise le procédé antique du cylindre qu’on fait rouler sur un support adapté, de l’argile molle par exemple, aujourd’hui sur une feuille de papier :
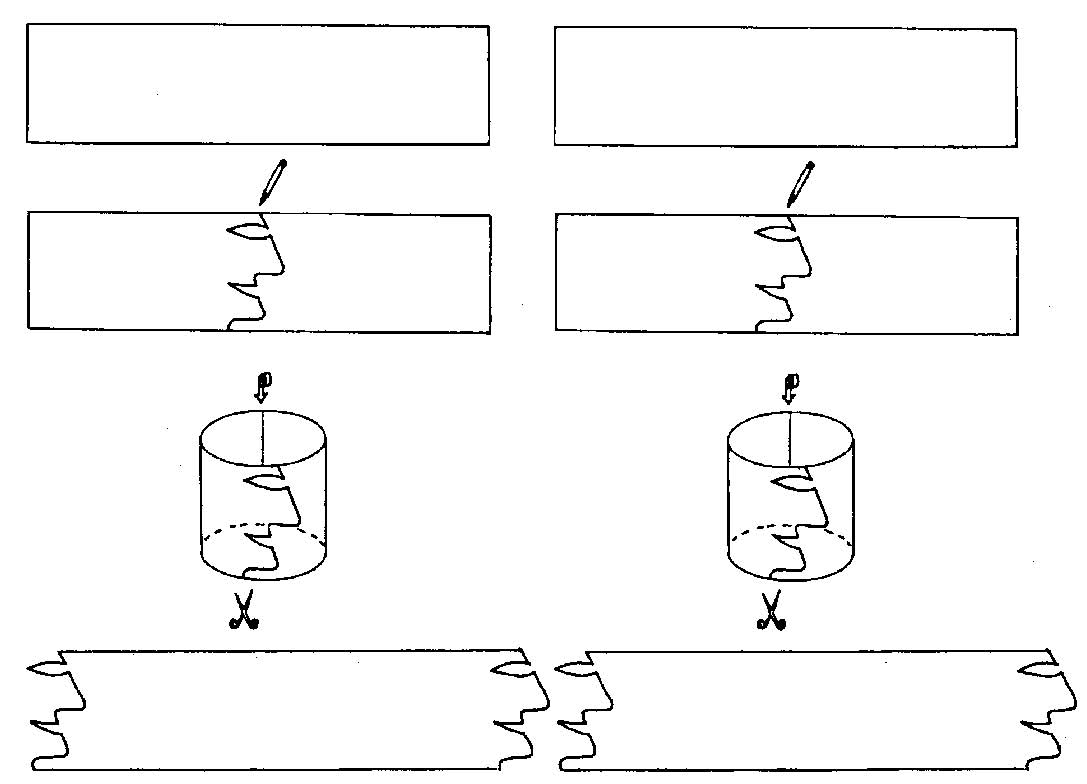
Le procédé du cylindre permet de réaliser un pavage dans la direction du roulement de ce cylindre, dont le cercle de base a pour périmètre l. Le motif, de longueur l, est collé sur le cylindre. Le roulement du cylindre imprime le motif de manière périodique. Les mathématiciens appellent alors ce cylindre une «orbifold ».
Voici une autre orbifold, plus savante, matérialisée par la sculpture suivante:

An orbifold is the orbit space of a manifold with a group action. Mathematically, the sculpture (as a solid, i.e., with the interior filled in) is the orbifold T3/ S3 – the quotient of the 3-torus by the symmetric group on 3 letters; equivalently, 3 unordered points on the circle (3 ordered points on the circle corresponding to the 3-torus, and ignoring the order corresponding to the
quotient map). The 3-dimensional interior corresponds to the points on the torus where all 3 coordinates are different, the 2-dimensional face correspond to the points on the torus where 2 coordinates coincide but the third is different, and the 1-dimensional edge corresponds to points on the torus where all three coordinates are equal.
The sculpture Topological III, by American artist and physicist Robert R. Wilson, is at the entrance to the Harvard Science Center building, Harvard University, Cambridge, Massachusetts.
Musical triads can be modeled as points in a certain 3-dimensional orbifold, which may be realized as a solid torus with triangular cross-section and a twist.
https://en.wikipedia.org/wiki/Orbifold
II.4 Surfaces anciennes et modernes :quelques incarnation artistiques
Supposant que nous avons une connaissance suffisante des techniques théoriques et pratiques de pavage sur sol, la question se pose néanmoins de savoir ce qu’on entend par ce terme, sol, d’en reconnaître les propriétés, de parvenir à classer les différents types qu’on en peut concevoir.
Quelle signification le mathématicien en particulier accorde-t-il au terme sol ? Il entend par là une surface, c’est-à-dire un domaine, souvent immense, mais qu’on peut diviser en petites cartes locales de sorte que, presque partout, on peut rapporter la position d’un point à deux coordonnées locales, appelons-les la longitude locale x et la latitude locale y. Les surfaces sont ainsi des objets dont on dit que la dimension topologique est 2.
Le recollement des cartes locales permet d’obtenir la surface dans sa globalité.
Le nombre des surfaces est infini. Jetons un coup d’œil rapide sur quelques exemples de sols, de surfaces, enveloppes de mondes habités, sur lesquels peuvent se déplacer, marcher des êtres qui peut-être nous ressemblent.
Voici d’abord les surfaces classiques (celle du plan n’est pas représentée) qui n’ont pas de singularité pointue. Une de leur caractérisation principale est leur courbure locale dite totale, car elle prend en compte en chaque point de la surface les courbures des courbes les plus significatives qui passent par ce point. Les trois principales surfaces sont le plan de courbure nulle, la sphère unité de courbure 1, l’hyperboloïde « unité » de courbure -1 – un hyperboloïde s’obtient par rotation d’une hyperbole autour de l’un de ses axes de symétrie. Un théorème dit d’uniformisation dit qu’en dehors de singularités, la forme locale de toute surface est soit celle soit du plan, soit celle locale de la sphère, soit celle locale de l’hyperboloïde. Il n’y a donc que ces trois géométries fondamentales possibles sur une surface quelconque.
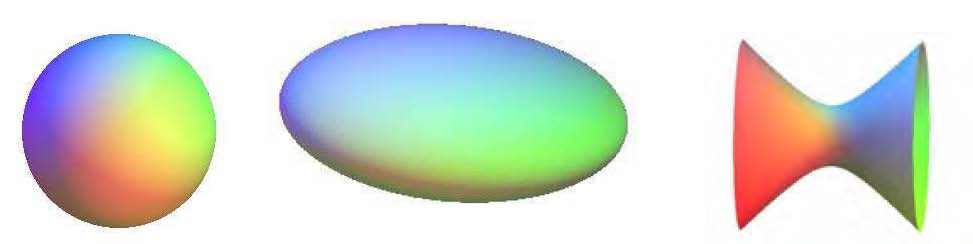
Sphère ellipsoïde hyperboloïde à une nappe

Hyperboloïde à deux nappes
Une autre caractérisation des surfaces est leur indice dit d’Euler-Poincaré, qui détermine de leur genre (leur nombre de trous intrinsèques). Une troisième de leurs caractéristiques est leur orientabilité.
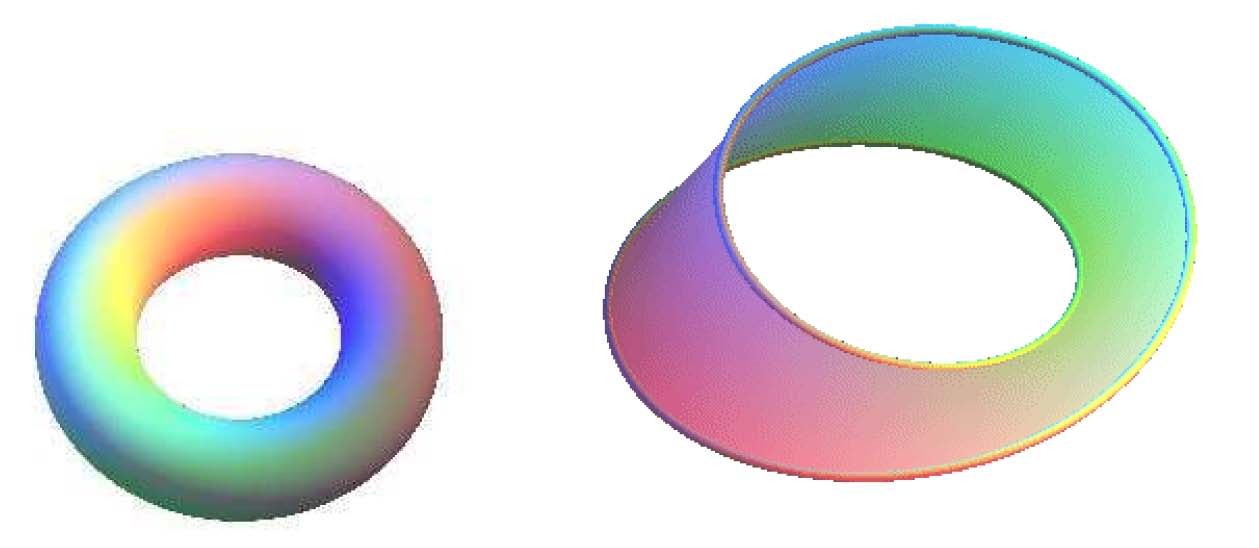
Tore Ruban de Moëbius (orientable, genre 1) (non orientable, genre 1)
https://www.mathcurve.com/surfaces/
Voici d’autres surfaces non orientables dont les noms sont bien connus. On ne peut les représenter dans l’espace usuel qu’à la condition de faire en sorte qu’elles se croisent elles-mêmes en des lignes particulières :
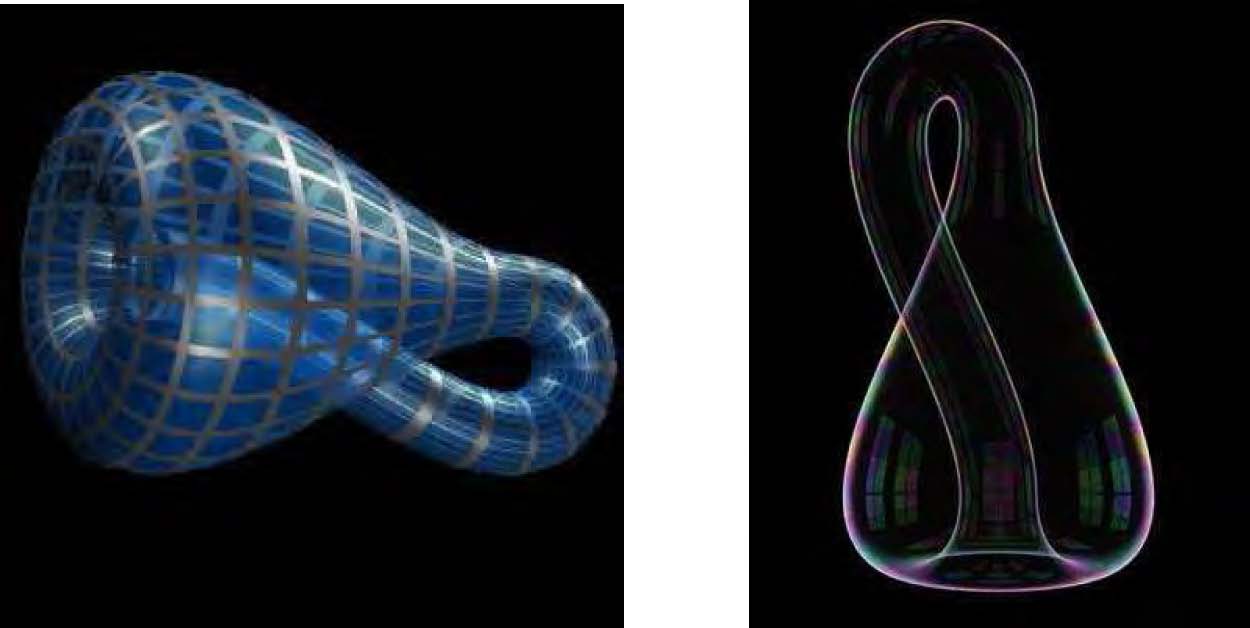
La fameuse bouteille de Klein (1882) (à gauche celle créée par Banchoff & alii), à droite celle créée par John Sullivan) (https://www.mathcurve.com/surfaces/klein/klein.shtml )
ici gravée par Jeener
Surface de Boy (Jeener)
Voici maintenant les premiers éléments de la famille des polyèdres, les cinq solides platoniciens, dont les bords sont des surfaces présentant des singularités pointues. L’indice χ(P) d’Euler-Poincaré d’un polyèdre quelconque P se calcule par la relation :
χ(P) = Nombre de faces – nombre d’arêtes + nombre de sommets
.
Il est arrivé, dans l’antiquité, que l’un de ces polyèdres, le dodécaèdre en particulier, ait donné sa forme à des dès à jouer, notamment chez les Etrusques et chez les Romains. Mais c’est dans les œuvres de la Renaissance que les polyèdres furent surtout représentés. Quatre d’entre ces œuvres sont célèbres : les dessins faits par Léonard de Vinci pour illustrer l’ouvrage de son collègue Fra Luca Pacioli, mathématicien auteur d’un ouvrage renommé, Divina Proportione (1509), le tableau de Jacopo de Barbari représentant Pacioli, la gravure de Dürer intitulée Melancholia (1514), et la sculpture sur bois dans l’église Santa Maria di Organo à Veronne.

Melancholia
 Fr
Fr
a Luca Pacioli par Jacopo de Barbari Eglise Santa Maria in Organo, Véronne
De nos jours, en dehors de Escher, seul le peintre Salvatore Dali a repris le flambeau d’inscrire les polyèdres dans ses toiles, par exemple un icosaèdre dans son tableau de 1955
« La Cène -Le dernier Repas » :

Mais sa toile plus célèbre est celle de la Crucifixion, sous-titrée Corpus hypercubicus, où sert de croix le développement dans l’espace tridimensionnel du cube de l’espace quadridimensionnel.

Une des classes de surfaces parmi les plus anciennes est celle des surfaces réglé
es -comme le cylindre et le cône -engendrées par des droites s’appuyant sur une courbe. Faciles à réaliser, elles sont abondamment utilisées en architecture.
Parmi les plus célèbres sont l’hélicoïde, engendrée par les droites s’appuyant sur une hélice, l’hyperboloïde à une nappe et le paraboloïde :

Les Essarts-le-Roi Vladimir Choukhov, Nijni Novgorod, 1896
Ces deux objets mathématiques ont fait les délices de la brillante école architecturale espagnole. L’architecture de la fameuse église de Barcelone construite par Gaudi (1852-1926), La Sagra Familia, repose sur l’emploi d’une multitude d’hyperboloïdes à une nappe. Quant au tandem Candela et surtout Calatrava, ils se sont fait une spécialité dans l’emploi du paraboloïde hyperbolique que l’on voit dans ces trois images :

 Pon
Pon
t sur le canal Hoofdvaart, Hollande Milwaukee Art Museum (Calavatra : 2004 1994-2001)
D’autres surfaces réglées, comme par exemple les cubiques de Cayley, ont inspiré les œuvres des sculpteurs Antoine Pevsner (1886-1962) et Naoum Gabo, frère du précédent.
La théorie des singularités différentiables du 20ième siècle a conduit sur la découverte de nombreuses autres surfaces réglées, comme le « parapluie de Whitney » et certains « ensembles de catastrophe de Thom ». Ces nouvelles surfaces peuvent être incarnées dans des architectures nouvelles.

x²z = y²
https://www.geom.uiuc.edu/zoo/features/whitney/
Voici maintenant des surfaces non polyédriques présentant à nouveau des singularités (le nombre et le type de singularité font partie des caractérisations de ces surfaces):

Derviche
aF+q= 0 où: F = h1h2h3h4h5, hi = cos(2π(i-1)/5)x -sin(2π(i−1)/5)y -z q = (1-cz)(x²+y²-1+rz²)² a, c, r sont des constantes adaptées 64(x−1)(x4−4x3−10x2y2−4x2+16x−20xy2+5y4+16−20y2)−5a(2z−a)[4(x2+y2+z2)+(1+3√5)]2= 0 a= √(5 − √5).
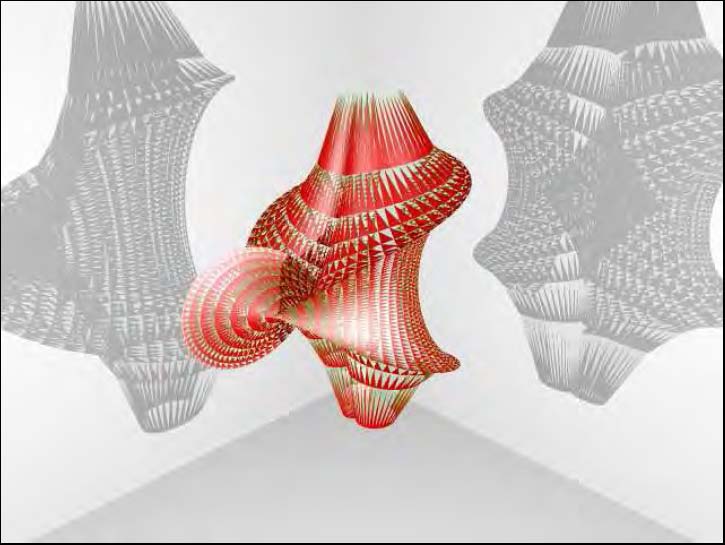
Surface de Kuen (de courbure -1) On y voit des courbes singulières
x=2[cosu + usinu]sinv /[1 + u²sin²v] y=2[sinu – ucosu]sinv /[1 + u²sin²v] z=log[tan(v/2)]+ 2cosv /[1 + u²sin²v]
https://jalape.no/math/kuengif.htm
Nous voyons maintenant la partie centrale de la même surface de Kuen, œuvre primée en 2009 par la National Science Foundation:

Songe d’un étudiant (Luc Bénard-Richard Palais)
Toutes les surfaces que nous avons rencontrées jusqu’à présent, sauf la dernière, celle de Kuen, sont dites algébriques, car on peut donner leur équation sous une forme polynômiale.
Une dernière classe importante de surfaces est celle des surfaces optimales, parmi lesquelles les surfaces dites minimales, comme l’est la sphère ou le sont des bulles de savon. Leur forme est celle qui assure une dépense minimale d’énergie pour les constituer. Reconnues depuis la fin du 18ème siècle, elles présentent bien sûr un fort intérêt pour la description et la compréhension des formes des objets du monde physique.

https://www.indiana.edu/~minimal/gallery/index/
Les surfaces optimales suivantes sont dues à John Sullivan, un maître de la transparence:

Polytope régulier en Bulles de savon Surface de Willmore
https://torus.math.uiuc.edu/jms/Images/

Retournement de la sphère à énergie minimale
La dernière image que voici est en quelque sorte une petite synthèse des surfaces révélées par les mathématiciens.

Luc Bénard-Richard Palais
(œuvre primée par la National Science Foundation) On « reconnaît » ici, de droite à gauche : en haut, une surface minimale 4-noïde, un breather, une surface de Boy, en bas, une bouteille de Klein, la surfacede Seivert-Enneper.
https://virtualmathmuseum.org/Surface/gallery_o.html#PseudosphericalSurfaces
Si les surfaces classiques, sphères, cônes, hyperboloïdes ont trouvé depuis longtemps leur incarnation dans l’architecture, ce n’est pas encore le cas de surfaces découvertes plus récemment.
Dans le projet de musée des mathématiques éclaté que j’ai conçu, certaines de ces surfaces sont présentes. Ce projet, tout comme les expositions mathématiques et arts, ou bien cette conférence, a d’abord pour but de contribuer à affaiblir les barrières psychologiques qui séparent les publics des mathématiques. Dans ce projet, un grand parc verdoyant de promenade est égayé par des petits bâtiments, des folies en terme architectural, entièrement définies et décorées par les mathématiques. Elles illustrent chacune un chapitre des mathématiques, des concepts, des faits. On se promène dans ce parc d’abord pour le plaisir des yeux, et pour la détende de l’esprit, surpris par les décors.
J’ai pensé à 10 folies, en hommage aux Pythagoriciens, qui attribuaient une valeur sacrée à la suite des quatre premiers nombres, 1, 2, 3, 4 et à leur somme le nombre 10.
Ce projet n’est pas encore venu à réalisation, il est en tout cas présent en images, quoique encore bien imparfaites, à l’état d’esquisses pourrait-on dire. Je présenterai celles de la première des folies, à l’architecture très classique,


et, sous la forme d’une animation, présente sur le site https://christophe.delsart.free.fr/ARPAM/, celles de la dernière des folies, une surface de Boy établie d’après l’équation d’Apéry, et dont l’architecture n’a jamais encore été réalisée.
1. Sur Dali Les citations sont extraites de son ouvrage : Salavador DALI : Oui, Méthode paranoïaque-critique et autres textes,
Denoël/Gonthier, Paris, 1971 Les images sont extraites de l’ouvrage : DALÍ : (Robert Descharnes-Gilles Néret Ed.) Taschen GmbH, Köln, 2010 Deux mathématiciens ont déjà quelque peu commenté Dali :
Slavik JABLAN : Geometry in Dali’s work : a play with ambiguity
Marc CHAPERON : Une hirondelle en hiver, Pour La Science n° 338, Décembre 2005. où est présentée cette œuvre, la dernière du peintre :

Les connaisseurs de la théorie mathématique des catastrophes y reconnaîtront une figure familière et emblématique. On y voit la pureté de la ligne, la double spirale de l’ouïe du violon, lui-même présent à gauche. Tout ceci fait corps, car le violon est aussi l’instrument qui, à mon oreille tout du moins, est celui qui nous faite entendre les sons les plus purs. Violon, dont un maître fut Paganini, par ailleurs doué pour les mathématiques, mathématiques au profit desquelles le maître Hassler Whitney sacrifia le violon. Notons que l’ouïe du violon est liée tant physiquement que presque mathématiquement aux phénomènes vibratoires.
2. Le monde hyperbolique
Soit un randonneur, se promenant par une belle journée ensoleillée, sur le sol d’un domaine de courbure -1 : ce domaine local est celui par exemple d’un col entre deux sommets. La forme locale du domaine est celle d’une selle de cheval ; vous pouvez l’obtenir en sectionnant habilement un hyperboloïde à une nappe :

Hyperboloïde à une nappe col, selle de cheval
La géométrie sur ce domaine est, rappelons-le, dite hyperbolique.
Un hyperboloïde à une nappe est engendrée par la rotation d’une hyperbole autour de l’axe de symétrie ne la rencontrant pas :
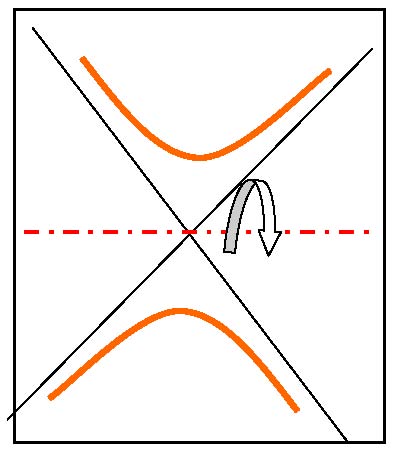
Si l’on fait tourner l’hyperbole, cette fois-ci autour de l’axe de symétrie qui la coupe, on obtient une autre version de l’hyperboloïde appelée l’hyperboloïde à deux nappes:
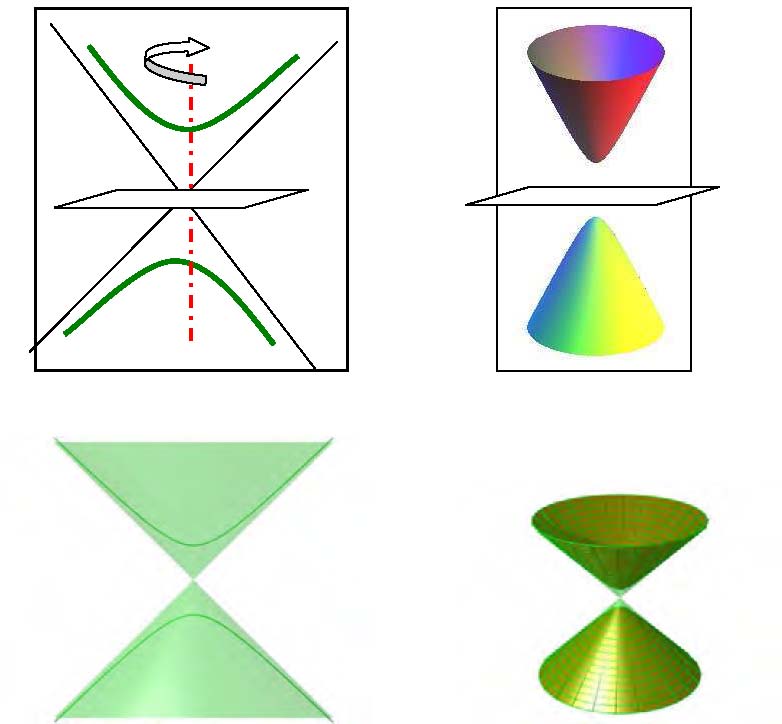
Dessins de Jos Leys
Le plan perpendiculaire à l’axe de rotation et passant par le centre de symétrie est le « plan équatorial » : sur cet l’écran, sur cette toile, sera dessinée, à la manière de Dürer, une image du contenu par exemple de la nappe supérieure rouge de l’hyperboloïde.
Les mathématiciens appellent « projection stéréographique » ce procédé. Il consiste à placer une source lumineuse au pôle sud. L’ombre bleue (figure suivante) de la partie supérieure, de la nappe supérieure de l’hyperboloïde sur l’écran est un disque, appelé « disque de Poincaré », mais introduit antérieurement par Beltrami.
Une hyperbole, située à l’intersection de l’hyperboloïde et d’un plan passant le centre du disque, a pour ombre dans le disque un cercle ou un segment de droite si le plan passe par l’axe de l’hyperboloïde.
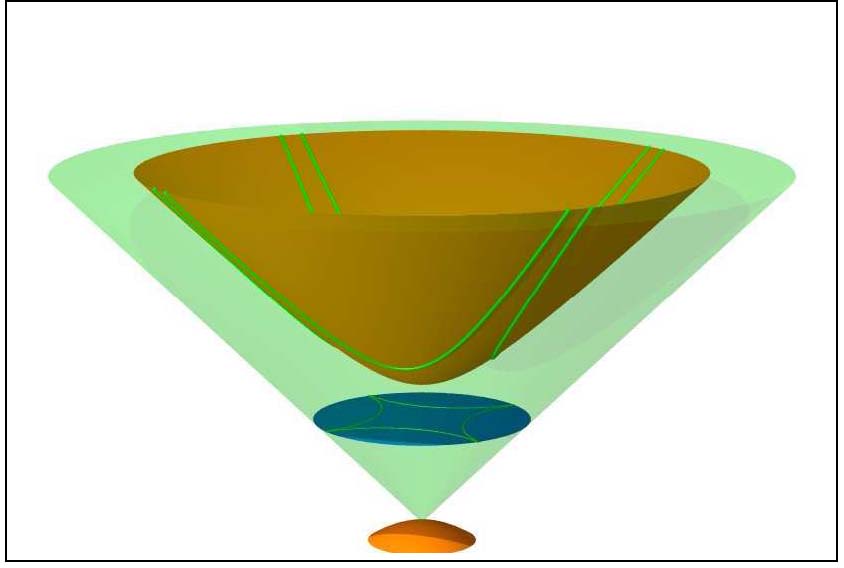 d
d
Extrait des ÉLÉMENTS POUR L'ÉTUDE DE FAISABILITÉ ARCHITECTURALE ET MUSÉOGRAPHIQUE du projet ARPAM (1992) :
Le descriptif exact de la coupole et du vitrail sera établi en liaison avec le constructeur. Les indications théoriques suivantes seront utiles: les arcs du vitrail situés sur l'hyperboloïde S sont à l'intersection de celui-ci avec des plans passant par l'origine et d'équation générique :
a x + b y +c z = 0. Par projection stéréographique de pôle sud sur le plan horizontal (u,v) passant par l'origine, ces intersections deviennent des cercles d'équation
(u + r)2 + (v + s)2 = r2 + s2 -R2
où r = a R/c , s = b R/c . Ces cercles sont orthogonaux au cercle C qui borde le domaine intérieur D de la projection stéréographique.
D étant muni de la métrique de Poincaré
- ds2 = 4 R4(du2 + dv2)/(u2 + v2 - R2)2
la longueur hyperbolique de OPo, où Po de coordonnées (u,0) est l'image d'un point Mo de S supposé situé dans un plan vertical y = 0, a pour valeur
d = R Log ((R + u)/(R - u )). Cette longueur d est aussi la longueur euclidienne de l'arc OMo tracé sur S.
De manière générale, le point P(u,v) est l'image du point M (x,y,z) où x = 2R2u/(R2 - u2 - v2) ; y a la même expression que précédemment où l'on remplace u par v ; z = x/u - R. La courbure de l'arc d'hyperbole z2 -x2 = R2 au point (z,x) a pour valeur k(z,x) = R2/(x2 + z2)3/2.
Remerciement : Ce texte s’est ouvert sur la photographie d’un coquillage spiralé découvert à Saverne. Nous le fermons ici en remerciant la personne qui nous a fourni cette image, et n’est autre que Jean Constant.